Algorithm - 평행

문제

점 네 개의 좌표를 담은 이차원 배열 dots가 다음과 같이 매개변수로 주어집니다.

• [[x1, y1], [x2, y2], [x3, y3], [x4, y4]]

주어진 네 개의 점을 두 개씩 이었을 때, 두 직선이 평행이 되는 경우가 있으면 1을 없으면 0을 return 하도록 solution 함수를 완성해보세요.

입출력 예

dots	result
[[1, 4], [9, 2], [3, 8], [11, 6]]	1
[[3, 5], [4, 1], [2, 4], [5, 10]]	0

풀이

나는 수학을 잘하지 못한다. 그래서 처음부터 “기울기”를 구할 생각을 하지 못했다.
처음 눈에 들어온 부분은 위 입출력 예의 첫번째 부분이다.

• 평행인 dots(result가 1인 dots)는 그렇지 않은 dots(result가 0인 dots)와 무슨 차이점이 있을까?
  • Index0,1의 각각의 x, y의 차([1 - 9, 4 - 2] = [-8, 2])가 Index2,3의 각각의 x, y의 차([3 - 11, 8 - 6] = [-8, 2])와 같다.
  • 이 부분을 보면서 어떠한 공식이 있다고 생각을 했다.

기울기 공식

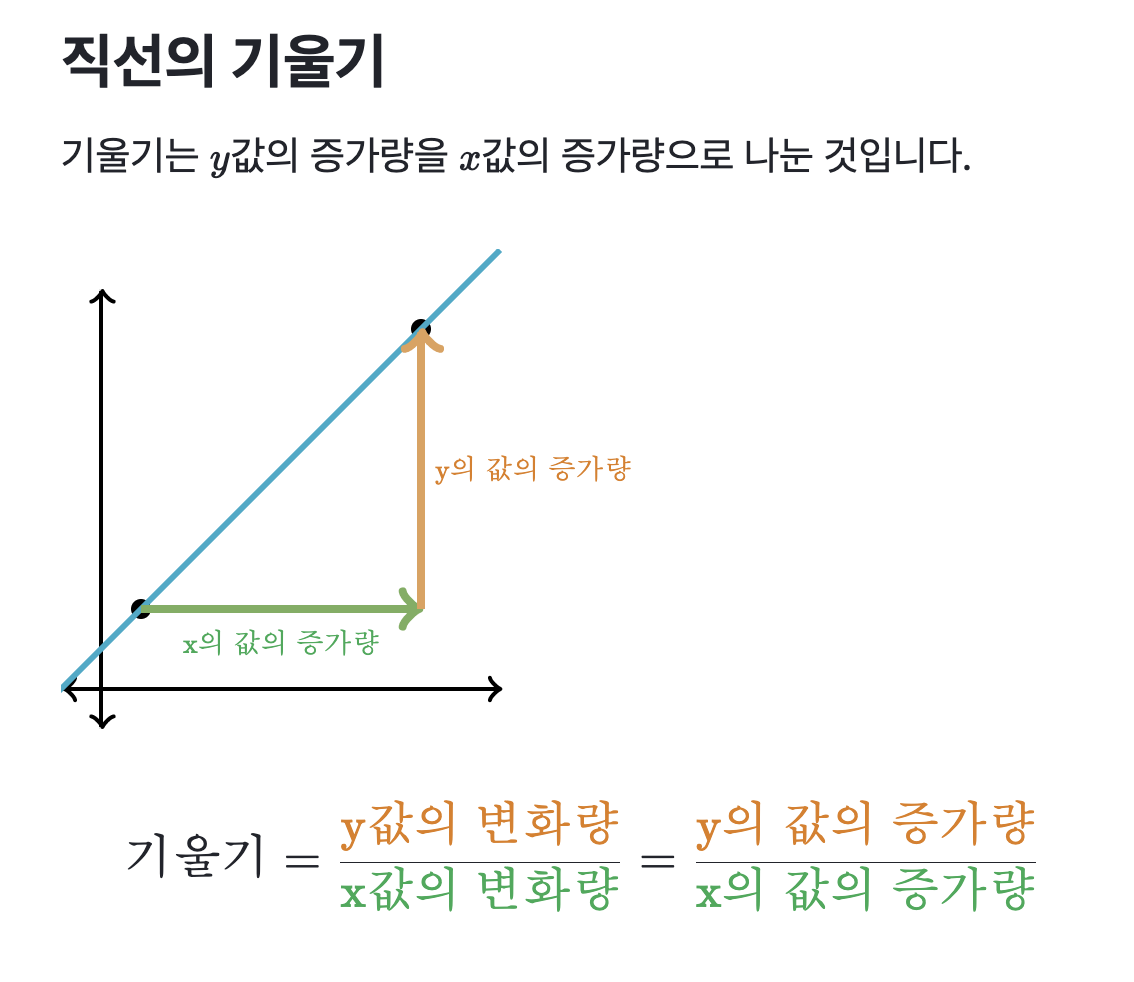
역시 검색을 해보니 기울기에 관한 공식이 있다. 이제 평행인 dots의 비밀에 대해 이해가 되었다.

• x(or y)의 변화량 : 변화된 곳의 지점 - 변하기 전의 지점
  • => Index0,1의 각각의 x, y의 차([1 - 9, 4 - 2] = [-8, 2])가 Index2,3의 각각의 x, y의 차([3 - 11, 8 - 6] = [-8, 2])
• point로 주어지는 배열은 총 4개
• 네 개의 포인트를 이어서 2개의 선을 만들게 되면 총 3번을 이을 수 있다.
• 하나라도 평행이 되는 2개의 선이 있으면 answer는 1을 리턴.

내 코드

function solution(dots) {
    // 선을 이을 두 좌표값의 (dots[0]x1 - dots[1]x2), (dots[0]y1 - dots[0]y2)의 값이 같아야 한다.
    // 첫번째 인덱스의 (배열의 첫번째 인덱스)와 두번째 인덱스의(배열의 첫번째 인덱스)를 빼서
    // 그 값이 다른 두 값의 차와 같아야 함.
    // y값의 증가량 / x값의 증가량 
    var answer = 0;
    let result = [];
    
    const compareLean = (point1, point2, point3, point4) => {
        const lean1 = (point1[1] - point2[1]) / (point1[0] - point2[0]);
        const lean2 = (point3[1] - point4[1]) / (point3[0] - point4[0]);
        
        if(lean1 === lean2) {
            result.push(true);
        }
    }
    
    compareLean(dots[0], dots[1], dots[2], dots[3]);
    compareLean(dots[0], dots[2], dots[1], dots[3]);
    compareLean(dots[0], dots[3], dots[1], dots[2]);
    
    if(result.length > 0) {
        answer++;
    }
    
    return answer;
}

결과

다른 사람의 풀이

function solution(dots) {
    if (calculateSlope(dots[0], dots[1]) === calculateSlope(dots[2], dots[3]))
        return 1;
    if (calculateSlope(dots[0], dots[2]) === calculateSlope(dots[1], dots[3]))
        return 1;
    if (calculateSlope(dots[0], dots[3]) === calculateSlope(dots[1], dots[2]))
        return 1;
    return 0;
}

function calculateSlope(arr1, arr2) {
    return (arr2[1] - arr1[1]) / (arr2[0] - arr1[0]);
}